引言

　　在統計學中，主成分分析法（PCA）是一種可以將多維數據集轉換為低維數據集的技術，以便更有效地進行可視化、分析和理解數據。隨著數據科學和機器學習的不斷發展，PCA已成為一種廣泛使用的技術。本文以"2024精準資料免費大全"為主題，介紹輕量版8.53的主成分分析法，并提供詳細的步驟和應用案例，旨在幫助研究人員和實踐者更深入地理解和應用這一技術。

主成分分析法原理

　　主成分分析法是一種基于特征值分解和線性代數的統計技術。其目標是找到數據中的主要變換方向，這些方向被稱為“主成分”，它們是線性無關的，并且按照方差的大小排序。通過將數據投影到這些主成分上，我們可以降低數據的維度，同時保留盡可能多的信息。

輕量版8.53的特點

　　與傳統的主成分分析法相比，輕量版8.53具有以下特點： 1. 高效：計算速度快，適合處理大規模數據集。 2. 簡單：使用更少的參數和算法步驟，易于理解和實施。 3. 靈活：可以根據不同的數據特性和需求進行調整。 4. 可擴展：可以輕松地與其他數據預處理和分析技術集成。 5. 免費：提供開源和免費的代碼庫，方便研究人員和實踐者使用。

PCA輕量版8.53步驟

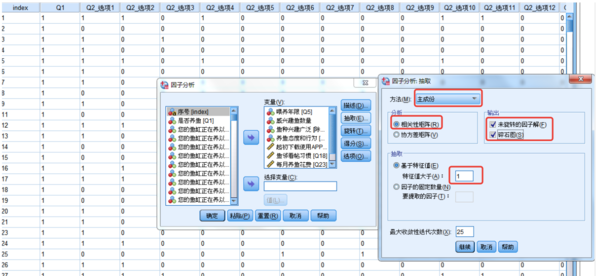
　　以下是使用輕量版8.53的主成分分析法進行數據降維的步驟： 1. 數據預處理：對數據進行中心化（減去均值）和標準化（除以標準差）。 2. 計算協方差矩陣：計算數據的協方差矩陣，以衡量數據特征之間的相關性。 3. 特征值分解：對協方差矩陣進行特征值分解，得到特征值和特征向量。 4. 選擇主成分：根據特征值的大小選擇前K個主成分，這些主成分可以解釋大部分數據的方差。 5. 數據投影：將原始數據投影到選定的K個主成分上，得到降維后的數據。 6. 重構數據（可選）：如果需要，可以使用主成分將降維后的數據恢復為原始維度的數據。

應用案例

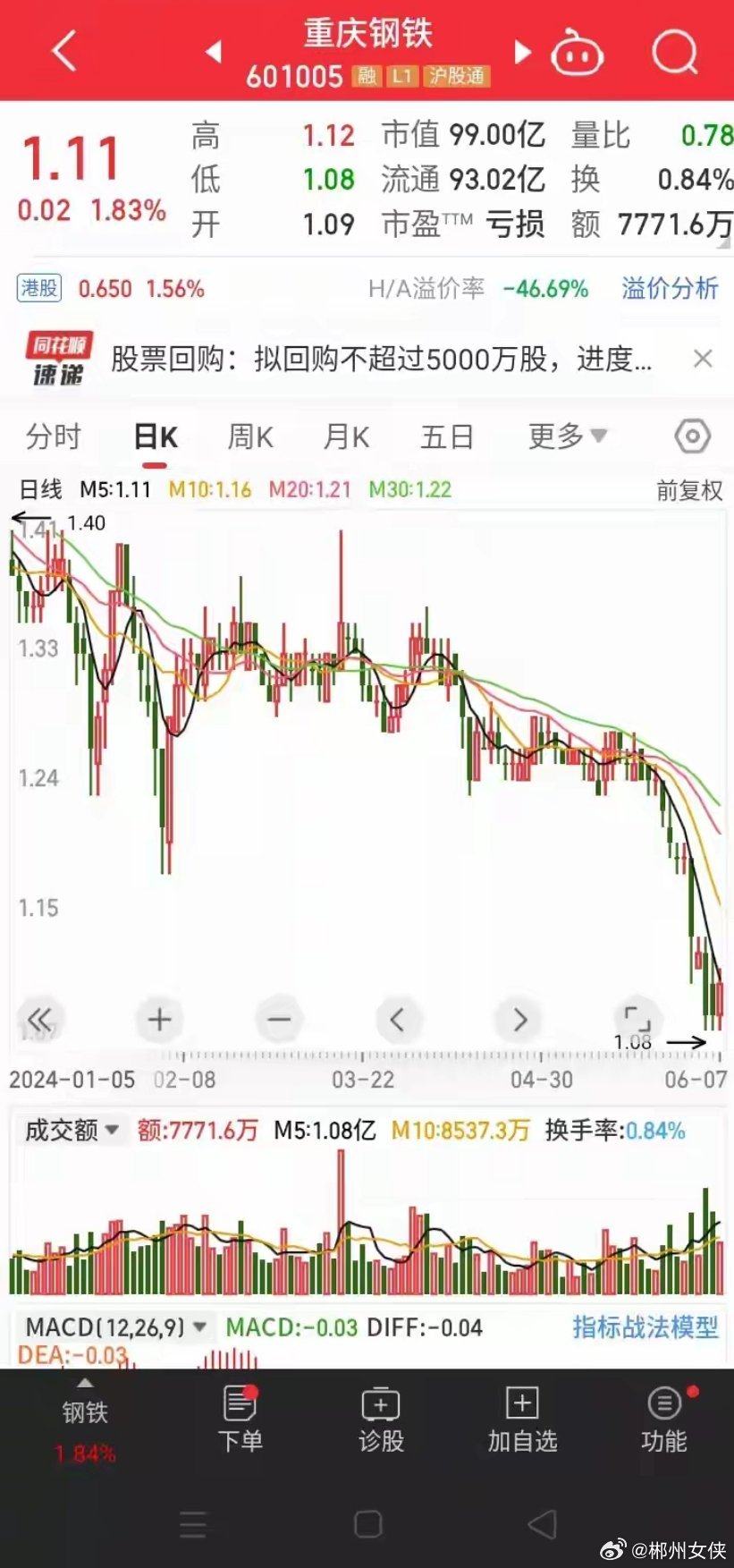
　　以下是輕量版8.53的主成分分析法在不同領域的應用案例： 1. 金融領域：用于股票價格的預測和風險評估，通過降維可以發現影響股票價格的潛在因素。 2. 生物信息學：用于蛋白質結構分析和功能預測，通過降維可以揭示蛋白質之間的相似性和差異。 3. 圖像處理：用于圖像壓縮和人臉識別，通過降維可以提取圖像的關鍵特征。 4. 語音識別：用于提取語音信號的特征，通過降維可以提供更高的識別準確率。 5. 推薦系統：用于提取用戶興趣和產品特征，通過降維可以提供更準確的推薦結果。

結論

　　主成分分析法是一種強大的數據降維技術，而輕量版8.53提供了更高效、簡單的方法來應用這一技術。通過遵循上述步驟和應用案例，研究人員和實踐者可以更好地理解和應用輕量版8.53的主成分分析法，從而在各自的領域中實現更好的數據理解和分析結果。

參考文獻

　　[1] Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.

　　[2] Jolliffe, I. T. (2002). Principal Component Analysis (2nd ed.). Springer.

　　[3] Abdi, H., & Williams, L. J. (2010). Principal Component Analysis. WIREs Computational Statistics, 2(4), 433-459.